1. Українська народна математика мала у
своєму арсеналі оригінальні способи зображення чисел. Одиниці позначалися
паличками, десятки — хрестиками, сотні — кружечками, тисячі — квадратиками. Що
ж до дробових чисел, то їх передавали переважно в усній формі з відповідними
назвами (половина, чверть, восьмушка, шістнадцятка та ін.). Письмово
(невеличкими горизонтальними рисками) зображалися лише найбільш уживані дроби.
Для написання
числових знаків використовували найрізноманітніші предмети (дощечки, палички).
Проте найчастіше для цього послуговувалися одвірками, дверима, стінами, на яких
малювали рисочки або карбували зарубки. Досить поширеним засобом для позначення
чисел були зарубки на невеличких дощечках, прямокутних брусках чи палицях. Такі
своєрідні "документи" використовували лісоруби, ремісники, ними
послуговувалися, позичаючи гроші, здаючи податки, засипаючи в амбари на
зберігання зерно тощо. Карбування у різних місцевостях України мало різні назви
(карбики на Поділлі, цурки на Полтавщині, раваші на Гуцульщині, бірки на
Київщині).
Випробування 1: Розгадайте
як підраховував лісник дерева в лісі і скільки дерев він нарахував на одній
ділянці, якщо в нього на листку було намальовано один квадратик, три кружечки,
шість хрестиків і чотири палички.
Розв’язавши
задачу, необхідно виписати серед множини слів пов’язаних із лісом послідовність
тих слів, які є цифрами числа у відповіді. Серед обраних слів Ви знайдете
підказку, де знаходиться наступна умова задачі та сюрприз.
1
|
Пожежа
|
2
|
Лісник
|
3
|
Кран
|
4
|
Дерево
|
5
|
рушниця
|
6
|
Ящик
|
7
|
Дошка
|
8
|
Земля
|
9
|
Вода
|
10
|
Дикі тварини
|
2. Українські селяни знали й деякі основи геометрії. Зокрема, вони мали уявлення про просту й ламану лінії, про властивості рівнобіжних ліній тощо. При будівництві хат та виготовленні бондарських виробів використовували властивості діагоналей прямокутника (щоб побудувати стіни під прямим кутом), обчислювали відношення довжини кола до діаметра (за останній приймали третину довжини кола). Бондарі та теслярі вміли користуватися циркулем. Розписуючи хати, побутові вироби, селяни послуговувалися різними геометричними фігурами. Українцям були відомі оригінальні прийоми визначення відстані до недоступного предмета, виміру площі земельних ділянок різноманітних форм. Знали й основи механіки, які використовували при будівництві хат, вітряків, культових споруд та ін.
Випробування 2. Скільки кінців у чотирьох палок? У п’яти палок? А у п’яти з половиною? У відповідь запишіть суму чисел. Правильно знайдена сума підкаже Вам номер кабінету у школі, де ви запитаєте про наступною задачу та отримаєте СЮРПРИЗ.
3. Своєрідною мірою врожаю служили: "віз" ("фура"), "сани", "снопи", "бабки", "кладні", "хрести". Народна арифметика починалася з лічби на пальцях рук, паличок, камінчиків, бобів чи квасолі. Однак спорудження будинків, виготовлення складних знарядь праці - воза, плуга тощо вимагали певних знань і навичок. Найпростіші форми рахунків застосовували при випасанні худоби на відгоні. Для цього служив "раваш" - прямокутний брусок з позначками - "карбами", половина якого вручалась пастухам, а друга залишалася у господаря. Хлібороби вимірювали величину поля (прямокутні й багатокутні), здійснювалися розрахунки під час будівництва інженерних споруд, запроваджувався облік у ткацтві - "чисниця" (3 нитки), "пасмо" (30 ниток), "моток" (90 ниток) тощо. Стародавні міри довжини та маси на практиці майже не вживаються, але їх часто можна зустріти в оповіданнях, повістях, книгах з історії. Назви мір довжини згадуються також і в прислів'ях: "Від горшка два вершка", "Коса сажень в плечах", "Міряє на свій аршин".
ВИПРОБУВАННЯ 3. КАЧАН КАПУСТИ
Колгоспниця принесла на базар качани капусти і продала трьом покупницям. Перша взяла половину всіх качанів і ще півкапустини. Друга купила половину качанів, що залишились і ще півкапустини. Третя покупниця взяла останній качан. Скільки качанів капусти винесла на базар колгоспниця?
Правильно знайдена відповідь буде паролем для людини, яка відповідає в школі за підрахунок качанів капусти. Назвавши їй пароль, Ви отримаєте наступну задачу та СЮРПРИЗ.
4. Міри маси і рідини
Споконвіку мірою для сипких продуктів - зерна, муки, круп - була не їх маса, а об'єм. Обмін здійснювали за правилом: однаковий товар вимірювався посудом однакової місткості. Так з'явилися "мірки". У Карпатах це був посуд (бочка) на 32 л зерна. Меншими одиницями - були "півлітра" (16 л) і "чвертка" (8 л). Ними могли міряти крупу або муку. Побутував й інший спеціальний посуд для мір - "міртук", а також "гелетка". Поширеною стала така міра, як "гарнець" ("горнець"), що містила 3,7 л і поділялась на чотири кварти. Сталою мірою був "корець" (96 кг). На Гуцульщині йому відповідав "кобельчи" ("кобель"), що поділявся на чотири "фердилі", а останній, у свою чергу, - на чотири "патралиці" (8 л). Велику кількість зерна зберігали у "кадовбах" (8 ц), різної місткості бочках (від 200 до 100 кг). Відповідно вони стали й мірою - "один кадовб", "одна бочка". Для муки ще з давньоруських часів існувала міра "мисль" ("мисель") – посуд, що мав вигляд дволітрової циліндричної бляшанки. З тієї доби залишилась у побуті українського населення Карпат міра "око" місткістю в одне відро (10 л). На Гуцульщині функцію "ока" виконував камінь масою 12 ок ("камінь вовни"). Рідину міряли: відром ("коновцею"), "порцією" (100 г), "михайликом" (до 900 г), "кватиркою" (до 250 г) тощо; сир - "грудками", "гелетками" (6-12 кг), "бербеницями" (32 кг), "беривкою" (16 кг).
ВИПРОБУВАННЯ 4. У першому корчаку є молоко, у якому масова частка жиру становить 2%, а в другому – молоко з масовою часткою жиру 5%. Скільки треба взяти крігелів молока з першого корчаку та скільки фелеїв з другого, щоб отримати 4,5 гарнеця, масова частка жиру в якому становить 3%.
Розв’язавши задачу Вам необхідно підійти до завідуючої нашої їдальні та назвати їй відповідь. Якщо ж відповідь правильна, то Ви отримаєте наступну задачу + СЮРПРИЗ
5. Логічні задачі
Десятки і сотні математичних задач на кмітливість переходили з покоління до покоління, з вуст у вуста, від народу до народу, з одних книжок в інші. Одна з перших цікавих книжок з математики "Задачі для вдосконалення розуму юнацького" приписується вченому монаху VIII ст. Алькуіну з Йорка, який працював директором школи при дворі франкського короля Карла Великого. Ця книга користувалася великим успіхом протягом майже цілого тисячоліття. З неї взято багато цікавих задач, які користуються популярністю і тепер (серед них - задача "про переправу через річку вовка, кози і капусти" та інші). В Україні теж відомий цілий цикл цікавих задач, в яких використані математичні поняття. В них виявляється розум, кмітливість і спостережливість нашого народу, відбито його щоденне життя. Нерідко такі задачі, що прийшли до нас з глибини віків, прикрашені добрим народним гумором, забарвлені національним колоритом. Відомий методист математики К. М. Щербина, який у 1929 р. у Харкові опублікував статтю "Народна математика і школа", вважав, що народні задачі, що їх найбільше використовують у побуті, можуть привчати дітей уважно, з інтересом ставитися до оточення. Прихильником використання народних задач у навчальному процесі у 60-х роках XX ст. в Україні була Л. М. Граціанська. У своїй праці "Нариси з народної математики України" вона зазначає, що саме в народних задачах і загадках відображаються певні математичні поняття, і наводить приклади таких задач. Ось одна з них: "Скільки нас є?" Сім, сімнадцять, без двох двадцять, семеро, троє, ще й малих двоє.
Випробування
5.
У ТЕМНІЙ
КІМНАТІ
Я зайшов у кімнату, щоб узяти з шафи свої черевики і
шкарпетки. У кімнаті спала сестра, і було дуже темно. Я добре знав, у якому
місці шафи знаходяться мої три пари черевиків - усі різних фасонів, і 12 пар
шкарпеток - чорних і коричневих. Мені не хотілось запалювати
світло, щоб не розбудити сестру. Справді, як черевики, так і носки я
знайшов на своїх місцях, але, повинен зізнатися у безладді - просто купу з 6
черевиків і купу з 24 шкарпеток. Скільки черевиків і скільки (щонайменше) мені треба
винести з темної кімнати до світлої, щоб забезпечити себе парою черевиків
одного фасону і парою шкарпеток одного кольору, при цьому фасон взуття і колір
шкарпеток мені були байдужі?
Розв’язавши
задачу Вам необхідно знайти особу в нашій школі, яка повязана із одягом та
назвати їх різницю квадратів кількості черевиків та кількості шкарпеток. У разі
правильно вказаної відповіді Ви будете нагороджені цінним ПРИЗОМ.

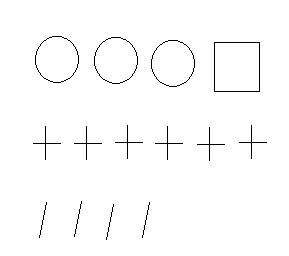







Комментариев нет:
Отправить комментарий