Контрольна робота з геометрії на тему: «Координати, геометричні перетворення та вектори у просторі», 11 клас

завантажити

ХХХІІ Міжнародний чемпіонат з розв’язування логічних математичних задач Чвертьфінал (заочний етап)

Правила організації та проведення Всеукраїнського етапу Міжнародного чемпіонату з розв’язування логічних математичних задач

Завдання чвертьфіналу ХХХІІ Міжнародного чемпіонату з розв’язування логічних математичних задач

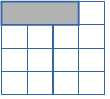
1. В кожен з кружечків впишіть по одному з чисел 1,2,3,4 (дивись малюнок) так, щоб сума кожних двох з них, які з’єднані відрізком, дорівнювала б числу, яке записане в квадратику, що знаходиться на цьому відрізку. Використайте всі чотири числа.

2. На малюнку зображено 18 маленьких квадратиків, але там ще є квадратики середнього розміру і великі квадратики. (Квадратики можна розглядати лише по лініях сітки.) Скільки всього квадратиків на малюнку?

3. На занятті математичного гуртка для малюків вчитель роздав кожному учню по одній такій картці, як на малюнку і по три олівці. Кожному по одному синьому, по одному жовтому і по одному червоному. Кожен учень розфарбовував фігурки на своїй картці так, щоб всі три були різних кольорів, але кожна фігурка фарбувалася лише одним кольором. Після перевірки вчитель виявив, що лише у двох учнів картки однакові. Скільки учнів максимально могло бути на цьому занятті гуртка?

4. В кутовій клітинці (дивись малюнок) сидить жучок, який може рухатись лише по сірих клітинках. На першій секунді він переповз на сусідню по горизонталі клітинку. На кожен такий хід жучок витрачає лише одну секунду. Переповзати він може лише на сусідню по вертикалі або сусідню по горизонталі клітинку.  Позначте плюсиком ті клітинки, в яких може опинитися жучок  рівно через 11 секунд після початку руху. Зауважимо, що після зробленого ходу жучок наступним ходом повертатися на щойно покинуту клітинку не може.

5. Позавчора мені було ще 7 років, а в наступному році мені виповниться 10 років. Вкажіть число і місяць мого народження.

6. Послідовність натуральних чисел має таку властивість: перше число дорівнює 718, а кожне наступне число дорівнює добутку числа 13 на суму всіх цифр попереднього числа. (Наприклад, друге число дорівнює 13х(7+1+8)=208.) Яке число записано на 2018 місці?

7. Мар’янка подарувала Михайлику книжку, яка складається з 225 сторінок, що утворюють три розділи. Сума всіх цифр номерів перших двох сторінок другого розділу, дорівнює сумі всіх цифр номерів останніх двох сторінок цього ж розділу і дорівнює 18. Скільки сторінок у другому розділі, якщо відомо, що їх більше двох?

8. Дано квадрат 4х4. Його покривають триміношками. Перше триміно уже поклали (дивись малюнок). Кожну наступну триміношку кладуть так, щоб вона обов’язково покривала хоча б одну раніше не покриту клітинку квадрата та розміщувалась строго по лініях сітки і не виходила за межі квадрату. Яку найбільшу кількість триміношок можна розмістити в квадраті, так, щоб виконувались всі вказані умови? (Зрозуміло, що триміношка може покривати один або два квадрата, які уже були покриті попередніми триміношками.)

9. Серед дітей, які відвідують шкільну баскетбольну секцію, 40 відсотків становлять хлопчики. Після того, як на секцію прийшло ще 6 нових хлопчиків, кількість дівчаток і кількість хлопчиків стала однаковою. Скільки всього дітей тепер відвідують секцію?

10. Лотерея містить 10000 квитків з номерами від 0000 до 9999. Вона проходить наступним чином: навмання обирають трицифрове число. Виграшними стають всі квитки, номери яких містять всі цифри обраного числа. Обрано число 116. Отже, виграшними квитками будуть ті і тільки ті квитки, номери яких містять не менше двох 1 і принаймні одну 6. Скільки виграшних квитків?

11. Катер плив по озеру від пристані А до пристані В. Коли він проплив половину шляху, то збільшив свою швидкість на 25відсотків. В результаті цього катер прибув до пристані В на пів години раніше, ніж якби весь шлях він плив з тією ж швидкістю, що і першу половину шляху. Скільки часу витратив катер на цю подорож? Відповідь запишіть у годинах та хвилинах, якщо потрібно, кількість хвилин округліть до цілих.

12. З пунктів А і В, відстань між якими 200 км, назустріч один одному виїхали два автомобіля зі сталими, але різними швидкостями. Швидкості виражаються цілими числами і різниця їх кратна 7. Через дві години після початку руху відстань від «швидшого» автомобіля до пункту В була у 5 разів менша, ніж відстань від «повільного» автомобіля до пункту А. Знайдіть швидкість «швидшого» автомобіля. Відповідь запишіть у км/год.

13. Знайдіть найменше натуральне число, яке кратне до 2018 і в записі якого в десятковій системі числення перші чотири цифри одиниці.

14. Дано квадрат, сторона якого 90 метрів. У квадраті проведено два відрізки, один з яких діагональ, а інший сполучає вершину квадрата з точкою, яка ділить протилежну сторону у відношенні 1 до 2, починаючи від діагонально протилежної вершини. (Дивись малюнок.) Ці два відрізки розбили квадрат на чотири частини. Знайдіть площу найбільшої з них. Відповідь запишіть у кв.м (якщо потрібно, округліть до цілих).

15. На малюнку зображено пірамідку, на кожній цеглинці якої – деяке натуральне число. Відомо, що число, записане на кожній з цеглинок, яка стоїть на двох інших, дорівнює сумі чисел, записаних на тих цеглинках, на яких вона стоїть. Якщо згідно цього правила записати числа на всі зображені на малюнку цеглинки, то сума всіх чисел на малюнку дорівнюватиме 2018. Яке число записано на сірій цеглинці?

16.  Дано чотирикутник, у якого два протилежних кути – прямі, а два інші такі, що один з них у два рази більший, ніж інший. Дві взаємно перпендикулярні сторони мають довжини по 100 метрів. Обчисліть площу цього чотирикутника. Відповідь запишіть у кв.м (якщо потрібно, округліть до цілих).

17. Число 2018 має наступну властивість: його половина число 1009 – просте і попереднє до нього число 2017 теж просте. Знайдіть число, яке більше, ніж 2018 і має таку ж властивість. У відповідь запишіть найближче з цих чисел до 2018.

18.  Фараон любить грати з числами в наступну гру. Записує деяке натуральне число. Знаходить суму кубів всіх його цифр і записує результат. Потім знову знаходить суму кубів всіх цифр щойно записаного числа і записує її. Наприклад, якщо початкове число 1012, то запис буде таким: 1012; 10; 1; 1 і т. д. Зрозуміло, що скільки б фараон не продовжував далі, нічого іншого крім 1 уже не з’явиться. Знайдіть число більше ніж 2018, але найближче до нього, забавляючись з яким по фараонські, на деякому кроці теж отримаємо 1.